视频先行

哔哩哔哩

YouTube

下面是视频内容的脚本文案原稿分享。

问题是真实存在的

大家好，我是扔物线朱凯。
刚才那个 0.1 + 0.2 不等于 0.3 的情况是真实存在的，不信你可以亲自试一下。我用的是 Kotlin，你换成 Java、JavaScript、Python、Swift 也都是这样的结果。要解决它也简单，在数值的右边加个 f，把它从双精度改成单精度的就可以了：


但这并不是一个通用的解决方案，比如有的时候情况会反过来：双精度的没有问题，而单精度的却有问题：


要知道，这些偏差都是开发里真实会发生的，所以了解这些问题的本质原因和解决方案是非常必要的——比什么内存抖动重要多了。
今天咱就说一下这个。不难啊，别害怕，你看进度条不长。

浮点数的范围优势和精度问题

大多数编程语言对小数的存储，用的都是浮点数的形式。浮点数其实就是一种科学计数法，只不过它是电脑用的、二进制的科学计数法：

十进制：500000
科学计数法：5 * 105
二进制：1111010000100100000
浮点数（二进制科学计数法）：1.111010000100100000 * 218

科学计数法的好处我们上学的时候老师就说过，可以用较少的数位来记录绝对值非常大或者非常小的数：

1000000000 -> 1 x 109
0.000000001 -> 1 x 10-9

但当你要记录的数位比较长的时候：

1000000001 -> 1.000000001 x 109
1.000000001 -> 1.000000001 x 100

科学计数法的优势就没了。所以科学计数法都会规定有效数字的个数，有效数字之外的就四舍五入掉了：

1000000001 -> 1.0 x 109 // 有效数字 2 位
1.000000001 -> 1.0 x 100 // 有效数字 2 位

这就造成了精度的损失。你看到一个 1.0 x 109，你不知道它是从 10 亿这个数转换过来的，还是从 9.6 亿或者 10.3 亿或者别的什么数转过来的，因为它们都可以写成 1.0 x 109。1.0 x 109 代表的不是 10 亿这一个数，而是它附近范围内的一大堆数，这就是精度的损失。不过这是故意的，科学计数法就是用精度作为代价来换取记录的简洁。
计算机的浮点数也是完全一样的道理。它本质上就是一种科学计数法，只不过是二进制的。比如，同样在 JVM 里占 32 位的 float (Float) 和 int (Int)，float 却可以表达比 int 更大的整数：

32 位的二进制数据只有 232 个取值，再加上还要区分正负，所以 int 的最大值是 231 - 1 也就是这个数：

2,147,483,647

但是 float 同样是 32 位，却能突破这个限制，赋值为这么大的一个数。别说 int 了，它的范围比 64 位的 long 还大：

除此之外，它还能表示小数：

小数代码。

怎么做到的？靠牺牲精度来做到的。float 虽然也是 32 位，但它会从里面拿出 8 位来保存指数值，也就是小数点的位置。8 位的指数可以达到 ±27 也就是 ±128，也就是小数点往左或者往右 128 个二进制位，换算成十进制是左右各 38 个十进制位。每移动一位就是放大或者缩小 10 倍，38 位呀，非常大的放大和缩小倍数了——int 只记录整数，不记录小数，但它最大的值也只是一个十位数：

2,147,483,647

这就是为什么 Java 和 Kotlin 的 float (Float) 可以保存某些很大的整数，因为它有专门的指数位：

但同样，它用这 8 位来保存指数，那么相应的它的有效数字就变短了，所以它的精度是比 int 要低的。这就导致某些 int 能表达的整数，float 却表达不了，比如 50000005（五千万零五）：

这个数虽然不长，但是精度——太高了。
虽然只是超出精度而不是超出取值范围，所以只显示了黄线警告而不会拒绝编译，但由于 Float 确实表达不了 50000005，所以在运行时只能在它的能力范围内拿一个最接近的数来进行使用，而无法使用这个数本身：


可能跟很多人的直观想法不太一样，为什么末位是 5 不行，但换成 4 就可以了？不是应该换成 0 才行吗？因为这是二进制的。我们看着这个数不够整、精度不够低，这是因为我们是十进制的思维，但只要二进制觉得它挺整的、觉得它没有超出精度范围就够了。

50000000: 10111110101111000010000000 // 有效数字 19 位，holde 得住
50000004: 10111110101111000010000100 // 有效数字 24 位，同样 hold 得住
50000005: 10111110101111000010000101 // 有效数字 26 位，hold 不住，「四舍五入」到 50000004

而 int 在这时候就很靠谱了，它是可以表达自己范围内的任何整数的，50000005 对它完全没问题：



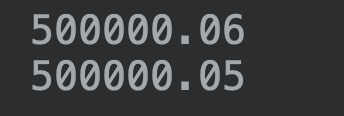
这是整数的情况，换成小数也是同样的道理。你用 Float 可以表示 500000，也可以表示 0.05，但无法表示 500000.05，因为它超出精度范围了：

不过二进制的数值并不能直接照抄十进制的小数点平移，所以你会发现加了小数点之后，500000.05f 会被「四舍五入」到 500000.06 而没有跟前面一样是 04：


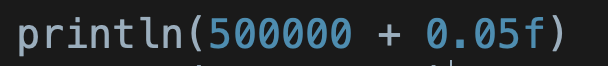
而如果把小数点往右移一位，改成 5000000.5，就直接不用「四舍五入」了：


你看，黄线没了，打印出来也是没问题的。因为 0.5 的二进制格式是 0.1，只用一位小数就表达了，所以整个数的精度没有超：

5000000.5： 10011000100101101000000.1 // 有效数字 24 位，hold 得住

同样是 32 位的大小，float 却比 int 少了 8 位有效数字长度，降低了精度，这是浮点数的弱点所在。而这个弱点也是故意的，因为这少了的 8 位用来存储指数了，也就是小数点的位置，改变指数的值就是改变小数点的位置——这也就是「浮点数」这个名字的含义。所以它是用精度作为代价，换来了更大的表达范围，让它可以表达小数，也可以表达很大的整数，远远超过 int 上限的整数。
浮点数可以用于表示小数，所以我们通常把它跟小数画等号；但其实对于一些数值特别大但有效数字并不多的整数的情况，也可以考虑使用浮点数。
不过就是刚才说过的，有得有失，浮点数的精度比较低。有多低呢？对于 float 来说，它的有效数字换算成十进制是 6-7 位。到了 8 位的时候，有很多数就无法精确表达了，比如 500000.05。而 double 的长度是 float 的两倍，有 64 位，它的精度就比较高了，它的有效数字相当于 15-16 位的十进制有效数字，能应付大部分的需求了——当然了如果你面向的是整数，那直接用 int 和 long 可能更好。

float vs double

说到这儿呢，咱就说一下关于 float (Float) 和 double (Double) 的选择问题。这其实是一个很容易出错但是经常被忽略的地方：float 的精度是比较低的，对于很多场景都可能会不够用。比如你如果用来做金额的计算，去掉小数点右边的两位之后，只有五位数字可以用了，也就是 10 万级的金额就不能用 float 了。那么在选择浮点数的类型的时候，你要时刻意识到这件事，在精度不够用的时候就选 double。
这其实也是为什么在 Java 和 Kotlin 里整数的默认类型虽然是更短的 int (Int) 而不是 long (Long)，但浮点数的默认类型却是更长的 double (Double)，而不是 float (Float)：

类型是 double (Double)。

因为 float (Float) 的适用场景过于受限了。
当然了如果你明确知道在某个场景下 float 够用了，那肯定用 float 更好，省内存嘛。
不过说到省内存我又要说了，不用过于纠结，对于很多场景来说，double 的双倍内存占用带来的性能损耗其实是很小的，小到完全可以忽略——你想想，32 位和 64 位才差多少？差 32 位，也就是 4 个字节，4 个 B，你省 1000 个才 4K 的大小——所以如果你真的想懒省事，全都用 double 大多数时候也是没有任何问题的。一个字符都 16 位了，也没见谁因为这个去精简软件界面的文字啊是吧。不过一些计算密集型或者内存密集型的工作，比如高频的循环过程或者某些需要大量复用的数据结构，还是得慎重考虑数值类型的啊，能用 float 就用 float。何止是 float 呀，在性能要求高的场景里，你甚至可能需要考虑要不要用单个 int 或者 long 变量来代替多个 boolean 变量去进行联合存储，以此来节约内存。而对于一般场景，double 虽然占双倍内存，但其实影响不大。

0.1 + 0.2 != 0.3 的问题

除了精度，浮点数还有个问题是，它是二进制的。这对整数还好，但对于小数来说，有很多十进制小数是无法转换成有限的二进制小数的。
二进制只有 0 和 1，所以它的 0.1 就是 2 的 -1 次方，也就是十进制的 0.5——二进制的 0.1 跟十进制的 0.5 是相等的；同理，它的 0.01 就是 2 的 -2 次方，也就是十进制的 0.25；而它俩相加的结果 0.11，对应的就是十进制的 0.75 。总之，你用 1 去反复地除以二，这些结果——以及这些结果的加和——都可以被二进制的小数完美表示。但如果一个小数无法被拆成这种形式，那它就无法被完美转换成二进制，比如——0.1。
可能有点反直觉，但十进制的 0.1 是无法被转换成一个有限的二进制小数的，它只能用一个无限循环小数来表达：

0.00011001100110011...

而且，浮点数并不会真的把它当做无限循环小数来保存，而是在自己的精度范围内进行截断，把它当一个有限小数来保存。这就造成了一定的误差。我们用的各种编程语言和运行时环境会对这种问题进行针对性优化，让我们尝试打印 0.1 的时候依然可以正常打印出 0.1，但在进行了运算之后，叠加的误差可能就会落在这种优化的范围之外了，这就是为什么在很多语言里，0.1 + 0.2 不等于 0.3，而是等于 0.300000……4：


同样的例子还有很多，比如 0.7 / 5.0 不等于 0.14：


注意了，我这里用的是不带 f 的小数，也就是用的 double。如果我给它们加上 f 也就是改用 float 的话，就恢复正常了：


这是为啥？这可不是因为 float 的精度比较低所以误差被掩盖了，而是对于这两个算式来说，恰好 float 的精度在截断之后的计算结果，误差依然在优化范围内，而 double 的掉到了优化范围之外而已。我如果把这个 0.1 换成 0.15，那状况就相反了，float 出现了问题，而 double 反而没问题了：


为啥？因为这次 float 掉到范围之外了。
所以，这种计算之后出现数值偏差的问题，是普遍存在的，它甚至不是精度太低而导致的，而就是因为十进制小数无法往二进制进行完美转换所导致的，不管你用多高精度的都会出这种问题，只要你用的是浮点数。我们用的各种编程语言的浮点数的实现，遵循的都是同一套标准，这个标准是 IEEE 推出的——要怪怪它去。

应对一：主动限制精度

那怎么办呢？一般来说有两种应对方向。
第一种是在计算之后、输出或者比较的时候，主动限制精度：

val a = ((0.1 + 0.2) * 1000).round() / 1000 // 0.3

if (abs(0.1 + 0.2 - 0.3) < 0.001) {
    ...
}

看着有点憨是吧？甚至有一丝羞耻。没办法，写吧！我也这么写的，大家都这么写的。浮点数就这样！

应对二：不用浮点数（不是开玩笑）

除此之外，另一个应对方向就是，你干脆别用浮点数了，用别的方案。比如 Java 有个叫 BigDecimal 的东西，就是专门进行精确计算用的。不过 BigDecimal 的使用没有浮点数这么简单，运算速度也比浮点数慢，所以大多数情况下，忍一忍，用浮点数还是会好一点。

总结

好，浮点数的东西大概就这么多。
下期有点想再说点 Compose 的东西了，不过也不一定，我看情况吧。如果你喜欢我的视频，还请帮我点赞和转发。关注我，了解更多 Android 开发的知识和技能。我是扔物线，我不和你比高低，我只助你成长。我们下期见！

版权声明

本文首发于：https://rengwuxian.com/float/

微信公众号：扔物线

转载时请保留此声明